週記(二十七)
2025-07-26
Table of Contents
Lord’s Paradox
悖論
ETS 的統計學家 Frederic M. Lord 在 1967 年提出著名的 Lord’s Paradox。1 這個悖論的情境如下。
一所大學想要調查學餐提供的飲食對學生的影響及其性別差異。 於是,他們記錄了每位學生在九月份入學時的體重 \(Y_{i}^{\mathit{Post}}\), 以及次年六月份的體重 \(Y_i^{\mathit{Pre}}\)。
兩位統計學家分別分析了這些資料。
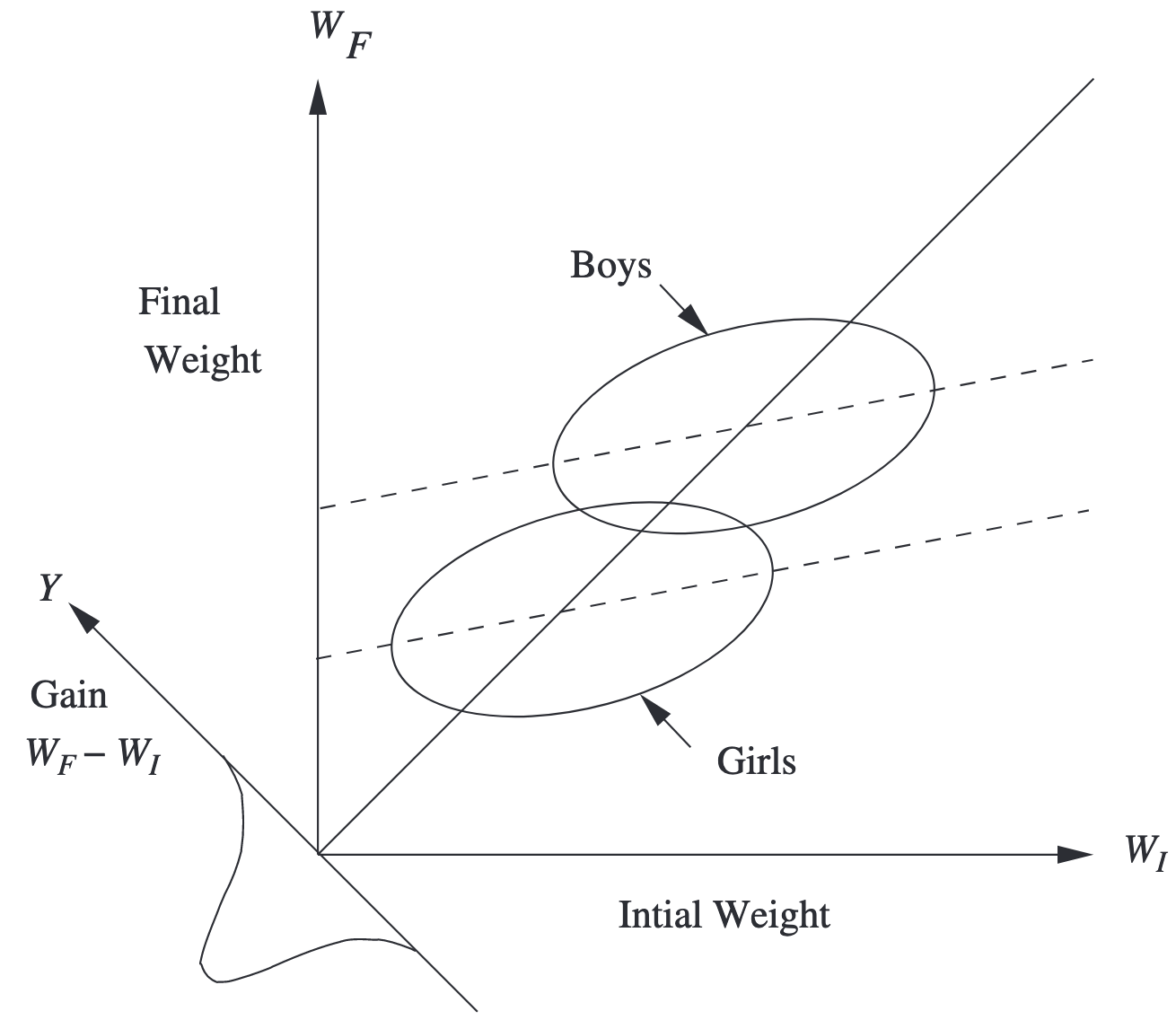
第一位統計學家發現,無論男生或女生,平均體重在剛入學時與學年結束時都保持不變。 如圖 Figure 1, 男生和女生的分佈的中心都落在 45 度線上, 表示初始體重與最終體重的平均值相等。 於是這位統計學家認為, 沒有證據表明學校飲食對男生或女生體重有所影響, 而因此男生與女生的體重增加亦沒有差異。
第二位統計學家則利用 analysis of covariance (ANCOVA) 進行分析。 他首先發現男生組和女生組的 \(Y_{i}^{\mathit{Post}}\) 對 \(Y_{i}^{\mathit{Pre}}\) 的迴歸線斜率相同 (迴歸線如 Figure 1 所示;這證成了使用 ANCOVA 進行分析), 而兩組迴歸線的截距之間的差異在統計上高度顯著。 換言之,他適配以下的線性迴歸: \[ Y_i^{\mathit{Post}} = \beta_0 + \beta_1 S_i + \beta_2 Y_i^{\mathit{Pre}} + \varepsilon_i, \qquad{(1)}\] 其中 \(S_i\) 是性別虛擬變數(\(S_i = 1\) 代表男生,\(S_i = 0\) 代表女生), 並發現 \(\beta_1\) 的估計值在統計上顯著。 因此,他認為在考慮初始體重以後,男生比女生顯著地增加了體重。 換言之,當我們選擇初始體重相似的一群男生和一群女生時, 我們會觀察到平均而言男生組比女生組的體重增加更多。
這樣就讓學校的營養師感覺很困擾了——這兩個統計學家的論證看起來都很合理,卻相互矛盾。
對此,Lord 的看法很悲觀, 他認為沒辦法期待任何邏輯或統計上的程序可以適當地考慮組間未受控制的既有差異:
研究者想知道,如果沒有預先存在的不受控制的差異,這些群體會如何比較。(The researcher wants to know how the groups would have compared if there had been no preexisting uncontrolled differences.)
但 Lord 認為,僅憑現有的資料,無法嚴謹地回答這個問題。
解讀
這個悖論歷來引起許多討論。
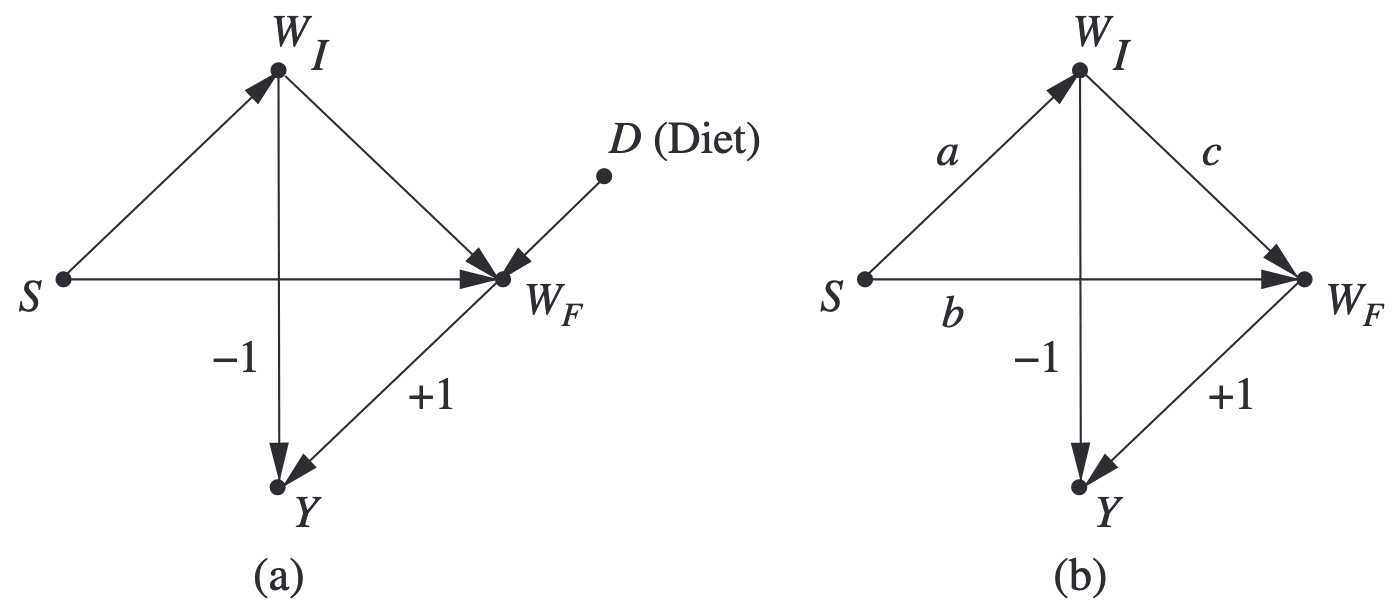
Pearl (2016) 認為兩個統計學家都正確,只是他們回答的問題不同。 在他看來,在 Lord’s paradox 中, 統計學家試圖回答的問題是「性別 \(S_i\) 對於體重增量 \(\Delta Y_i\) 的影響」。2 既然性別是天生的,我們不妨假定它就像是外生的一般。 因此,性別對體重增量的總效果可以被以下的期望值的差異所識別: \[ \text{Total Effect} = \operatorname{E}[\Delta Y_i \mid S_i = 1] - \operatorname{E}[\Delta Y_i \mid S_i = 0]. \] Pearl 認為這就是第一個統計學家所做的事。 第一個統計學家發現這個量為零,因此認為沒有證據表明性別對體重增量有影響。 考慮 Figure 2 (b) 的線性模型, 如果我們把變數都標準化,根據 Wright 的路徑分析公式, 總效果會是所有從 \(S_i\) 到 \(\Delta Y_i\) 的路徑的係數乘積之和: \[ \text{Total Effect} = b + ac - a. \]
另一方面,他認為第二位統計學家回答的是性別對於體重增量的直接效果 (排除掉透過初始體重的影響)。 在沒有其他干擾因子的情況之下, 直接效果同樣可以被以下的中介分析公式給識別: \[ \begin{align*} &\mathrel{\phantom{=}}\operatorname{Direct Effect}\\ &= \sum_y [\operatorname{E}[\Delta Y_i \mid S_i = 1, Y_i^{\mathit{Pre}} = y] - \operatorname{E}[\Delta Y_i \mid S_i = 0, Y_i^{\mathit{Pre}} = y]] \cdot P(Y_i^{\mathit{Pre}} = y \mid S_i = 0). \end{align*} \] 如果我們再假設線性模型,並把變數都標準化(如 Figure 2 (b))之下, 性別對於體重增量的直接效果可以簡化為 \[ \text{Direct Effect} = b. \] 總之,Pearl 認為這兩個統計學家都是對的,只是他們回答的問題不同。 如此,他算是解決了 Lord’s paradox。
Judea Pearl 更進一步認為,Lord 之所以困惑是因為 sure-thing principle 似乎被違反了:3 這裡違反直覺的地方在於, 有可能對於初始體重相似的一群男生和一群女生,男生的體重增量總是會比女生大, 但是整體而言,體重增量卻沒有性別差異嗎?
他在這裡指出這點,是為了連結 Lord’s paradox 和 Simpson’s paradox。 在他看來,這兩個悖論讓人困惑,都是因為誤解 sure-thing principle。 為了處理 Simpson’s paradox, Pearl (2009) 書中的定理 6.1 描述了一個修改版的 sure-thing principle:
一個行動 \(C\) 如果不會改變各個子群體的分佈, 而在每一個子群體都增加事件 \(E\) 的機率, 那麼這個行動 \(C\) 也必須增加整個群體中事件 \(E\) 的機率。
在 Simpson’s paradox 的經典例子中, 也就是說不可能存在一種同時增加男生和女生康復機率的療法, 不會增加整體的康復機率(除非這種療法會改變人的性別)。
回到 Lord’s paradox,為什麼這種違反因果直覺的情況會發生呢? 因為性別會影響初始的體重(平均而言男生的初始體重比女生來得重), 故即便對於初始體重相似的一群男生和一群女生, 男生的體重增量總是會比女生大, 整體而言體重增量還是可能沒有性別差異。 這個例子並不受 sure-thing principle 所約束。
Holland and Rubin (1983) 對此有不同觀點。 首先,他們認為在 Lord 的故事裡,統計學家想回答的問題是「飲食對於學年結束時的體重的影響」。 雖然我很喜歡 Pearl,而且以上那個故事是能夠自圓其說的, 但既然 Lord 一開始就說「一所大學想要調查學餐提供的飲食對學生的影響及其性別差異」, 這種解讀應該比較貼近這兩位統計學家的原意。
為了說明他們的觀點, 我們先定義潛在結果(potential outcomes)的符號。 令 \(Y_i^{\mathit{Post}}(1)\) 表示學生 \(i\) 在接受學校飲食後, 在學年結束時所測得的潛在體重, 而 \(Y_i^{\mathit{Post}}(0)\) 則表示學生 \(i\) 在沒有接受學校飲食的情況下, 在學年結束時所測得的潛在體重。 定義了潛在結果,我們就能定義學校飲食對於學生 \(i\) 在學年結束時體重的因果效應是 \[ Y_i^{\mathit{Post}}(1) - Y_i^{\mathit{Post}}(0). \] 而平均因果效應是 \[ \operatorname{E}[Y_i^{\mathit{Post}}(1) - Y_i^{\mathit{Post}}(0)]. \] 而男生與女生的平均因果效應分別是 \[ \begin{align*} &\operatorname{E}[Y_i^{\mathit{Post}}(1) - Y_i^{\mathit{Post}}(0) \mid S_i = 1], \\ &\operatorname{E}[Y_i^{\mathit{Post}}(1) - Y_i^{\mathit{Post}}(0) \mid S_i = 0]. \end{align*} \]
問題在於,在這個故事裡, 所有學生都接受學校飲食,因此我們觀察到的 \(Y_i^{\mathit{Post}}\) 都是 \(Y_i^{\mathit{Post}}(1)\), 而每位學生的 \(Y_i^{\mathit{Post}}(0)\) 都是反事實, 必須做出因果假設才有機會可以推論因果效應。
既然沒有學生沒有接受學校飲食, 我們很自然地需要利用學生們還未接受學校飲食時的體重 \(Y_i^{\mathit{Pre}}\) 的資訊。
Holland 與 Rubin 認為, 第一位統計學家的假設是如果學生沒有接受學校飲食, 他們在學年結束時的體重會和他們入學時的體重相同: \[ Y_i^{\mathit{Post}}(0) = Y_i^{\mathit{Pre}}. \] 換言之,他假設學年結束與開始的體重之間的差異全部都是因為學校飲食造成的。 基於這個假設,第一位統計學家認為 \[ \begin{align*} &\mathrel{\phantom{=}} \operatorname{E}[Y_i^{\mathit{Post}}(1) - Y_i^{\mathit{Post}}(0) \mid S_i = 1] \\ &= \operatorname{E}[Y_i^{\mathit{Post}}(1) - Y_i^{\mathit{Pre}} \mid S_i = 0] \\ &= 0. \end{align*} \] 也就是說,在第一位統計學家的假設下, 無論是男生或女生,學校飲食對於體重的影響都是零, 而因此男生與女生的體重增加亦沒有差異。
另一方面,第二位統計學家的 ANCOVA 模型 Equation 1 假設男女兩組的 \(Y_i^{\mathit{Post}}\) 對 \(Y_i^{\mathit{Pre}}\) 的迴歸線斜率相同,只差在截距;因為所有人的 \(Y_i^{\mathit{Post}}\) 都是 \(Y_i^{\mathit{Post}}(1)\),所以這相當於假設 \[ \operatorname{E}[Y_i^{\mathit{Post}}(1) \mid S_i = s, Y_i^{\mathit{Pre}} = y] = \alpha_s + \beta_2 y, \] 對照 Equation 1 的係數,我們發現 \(\beta_0 = \alpha_0\),\(\beta_1 = \alpha_1 - \alpha_0\),而兩式的 \(\beta_2\) 意義相同。 並且,第二位統計學家假設如果學生沒有接受學校飲食, 他們在學年結束後的體重會與入學時的體重有以下的線性關係: \[ Y_i^{\mathit{Post}}(0) = \alpha + \beta_2 Y_i^{\mathit{Pre}}. \] 其中,\(\beta_2\) 是 ANCOVA 模型 Equation 1 中 \(Y_i^{\mathit{Pre}}\) 的迴歸係數。 在這個假設之下,學校飲食對於學年結束時體重的平均因果效應是 \[ \begin{align*} &\mathrel{\phantom{=}} \operatorname{E}[Y_i^{\mathit{Post}}(1) - Y_i^{\mathit{Post}}(0)] \\ &= \operatorname{E}[Y_i^{\mathit{Post}} - (\alpha + \beta_2 Y_i^{\mathit{Pre}})] \\ &= \operatorname{E}[Y_i^{\mathit{Post}}] - \alpha - \beta_2 \operatorname{E}[Y_i^{\mathit{Pre}}]. \end{align*} \] 而男生與女生兩組的平均因果效應是 \[ \begin{align*} &\mathrel{\phantom{=}} \operatorname{E}[Y_i^{\mathit{Post}}(1) - Y_i^{\mathit{Post}}(0) \mid S_i = s] \\ &= \operatorname{E}[Y_i^{\mathit{Post}} \mid S_i = s] - \alpha - \beta_2 \operatorname{E}[Y_i^{\mathit{Pre}} \mid S_i = s], \end{align*} \] 因此兩組的平均因果效應之間的差異是 \[ \begin{align*} \operatorname{E}[Y_i^{\mathit{Post}} \mid S_i = 1] - \operatorname{E}[Y_i^{\mathit{Post}} \mid S_i = 0] - \beta_2 [\operatorname{E}[Y_i^{\mathit{Pre}} \mid S_i = 1] - \operatorname{E}[Y_i^{\mathit{Pre}} \mid S_i = 0] ]. \end{align*} \] 注意到這就是 ANCOVA 模型 Equation 1 中性別虛擬變數的迴歸係數 \(\beta_1\)。4 所以,在 \(Y_i^{\mathit{Post}}(0) = \alpha + \beta_2 Y_i^{\mathit{Pre}}\) 的假設下,第二位統計學家能得出飲食對於學年結束時體重的平均因果效應的性別差異是 \(\beta_1\)。
那到底哪個統計學家是對的呢?從以上的分析可以發現,這兩位統計學家的結論都建立在無法驗證的對於反事實結果的假設上。現有的資料並不直接拒絕任何一個統計學家的假設。
我覺得 Holland 和 Rubin 的看法確實解決了 Lord’s paradox,但相對地,這樣解讀就和 sure thing principle 有點扯不上關係,但我猜 Lord 確實有為此感到困惑。
題外話,細心的讀者可能已經發現,第一個統計學家計算飲食對於體重的效果的性別差異是這樣計算的: \[ \left( \frac{1}{n_1} \sum_{i: S_i = 1} Y_i^{\mathit{Post}} - \frac{1}{n_0} \sum_{i: S_i = 0} Y_i^{\mathit{Post}} \right) - \left( \frac{1}{n_1} \sum_{i: S_i = 1} Y_i^{\mathit{Pre}} - \frac{1}{n_0} \sum_{i: S_i = 0} Y_i^{\mathit{Pre}} \right), \] 其中 \(n_1\) 和 \(n_0\) 分別是男生和女生的樣本數。 這個式子事實上就是 difference-in-differences (DiD) 估計式,只是資料生成機制並非我們熟悉的 DiD 設計: 就算我們把男性或女性其中之一當成對照組,這很可能也不是一個好的對照組, 因為所有人都接受了學校飲食。 最近 Xu et al. (2024) 提到這類型的設計, 並把它命名為 factorial DiD。
綜合以上的討論,這個故事至少給我以下的啟示:
這兩位統計學家可以說都使用了「正確」的統計方法 (當然,在 2025 年的今天,統計軟體通常能一鍵完成這些分析)。 但是「正確」的統計方法不見得能在我們能信賴的假設之下回答我們感興趣的問題(特別是因果問題)。
因為缺乏適當的語言,這兩個統計學家都沒有清楚地定義研究問題, 定義他們關心的待估計量(estimand),5 說明他們為了識別這個量所做的假設, 以及他們的結論是如何從這些假設推導出來的。 而這些從事可信的科學研究的基本步驟。
人類能夠認識因果關係,真是一個奇蹟。 我們天生就有對於因果關係的直覺。 相對地,人類的直覺大概比較不擅長單純的機率和統計推理, 這種天性可能是讓我們感覺存在悖論的原因。 然而,當我們把問題重新描述成因果問題, 悖論就顯得迎刃而解。
他最著名的工作是開創心理計量的項目反應理論(item response theory)。↩︎
性別這類不可操弄的變數是否能被當成「原因」是另一個備受討論的問題,在此從略,我們先假設可以。↩︎
Sure-thing principle 最早由 Savage (1954) 提出,在這裡的意思大致上是指「在每個子群體中都成立的關係,不應在應用於整個群體時消失或改變符號」。↩︎
對線性迴歸模型 \[ Y_i^{\mathit{Post}} = \beta_0 + \beta_1 S_i + \beta_2 Y_i^{\mathit{Pre}} + \varepsilon_i, \] 我們有以下的 normal equations: \[ \operatorname{E}[\tilde{S}_i (Y_i^{\mathit{Post}} - \beta_1 \tilde{S}_i - \beta_2 \tilde{Y}_i^{\mathit{Pre}})] = 0, \] 其中 \(\tilde{X}_i = X_i - \operatorname{E}[X_i]\)。因此,迴歸係數 \(\beta_1\) 可以寫成 \[ \beta_1 = \frac{\operatorname{Cov}(S_i, Y_i^{\mathit{Post}}) - \beta_2 \operatorname{Cov}(S_i, Y_i^{\mathit{Pre}})}{\operatorname{Var}(S_i)}. \] 令 \(P(S_i = 1) = p\),則 \[ \begin{align*} &\mathrel{\phantom{=}} \operatorname{Cov}(S_i, Y_i^{\mathit{Post}}) \\ &= p \operatorname{E}[ Y_i^{\mathit{Post}} \mid S_i = 1] - p \operatorname{E}[Y_i^{\mathit{Post}}] \\ &= p \operatorname{E}[Y_i^{\mathit{Post}} \mid S_i = 1] - p \{ p \operatorname{E}[Y_i^{\mathit{Post}} \mid S_i = 1] + (1 - p) \operatorname{E}[Y_i^{\mathit{Post}} \mid S_i = 0] \} \\ &= p(1 - p) \{ \operatorname{E}[Y_i^{\mathit{Post}} \mid S_i = 1] - \operatorname{E}[Y_i^{\mathit{Post}} \mid S_i = 0] \}, \end{align*} \] 而 \[ \begin{align*} \operatorname{Cov}(S_i, Y_i^{\mathit{Pre}}) &= p(1 - p) \{ \operatorname{E}[Y_i^{\mathit{Pre}} \mid S_i = 1] - \operatorname{E}[Y_i^{\mathit{Pre}} \mid S_i = 0] \}, \\ \operatorname{Var}(S_i) &= p(1 - p). \end{align*} \] 因此 \[ \beta_1 = \operatorname{E}[Y_i^{\mathit{Post}} \mid S_i = 1] - \operatorname{E}[Y_i^{\mathit{Post}} \mid S_i = 0] - \beta_2 [\operatorname{E}[Y_i^{\mathit{Pre}} \mid S_i = 1] - \operatorname{E}[Y_i^{\mathit{Pre}} \mid S_i = 0] ]. \]↩︎
曾經有社會系的同學推薦給我這篇文章 Lundberg et al. (2021),我瀏覽過覺得作者說得不錯。↩︎
後記:寫文章的過程中,為了偷懶,我把 Holland 的論文丟給 ChatGPT o4-mini-high,希望它能幫我摘要,不過我發現它非常不瞭解因果推論。即便有原文,它還是無法理解 Holland 把學校飲食當成關心的原因,因此無法理解 Holland 所定義的潛在結果。除此之外,它似乎也很不理解 ANCOVA 係數的意義。突然很能夠理解為什麼計量課的學生們計量學得不好,畢竟他們是跟 ChatGPT 學的😅。