小學生筆記
週記 關於

週記（三十四）

2025-09-13

Table of Contents

故宮

好幾年沒去故宮，週六去了一趟。

最近故宮與大都會博物館合作， 在第二展覽廳展出一些大都會博物館的藏品。 這是要另外買票的，票價比故宮的第一展覽廳還貴 （而且其實學生去第一展覽廳也不用錢）。 雖然我不太了解西洋畫， 但是展品也不乏一些名人的作品， 例如馬締斯、雷諾瓦、梵谷等人。 對我來說最大的缺點是人太多、畫太少， 觀展的體驗並不是很好。

第一展覽廳最近有一個圍棋相關的展覽。 雖然我不懂圍棋， 但還是略看了一下。 幾乎所有展品都是宋元明清的書畫（特別是明清）， 讓我比較有印象的大概是文徵明的《溪山高逸圖卷》， 拖尾還有他寫杜甫詩《秋興八首》， 親眼看到覺得真的寫得很好看。

新網站

KM 說 CV 上可以放自己的 GitHub 頁面。 為了區隔個人和工作（？）的帳號， 我又重新弄了一個 GitHub 帳號和網頁。

現在這個網頁有一個缺點， 就是它承襲我早期寫的一些 CSS（再經過 LLM 魔改） 還有一些 LLM 寫的 JavaScript， 疊床架屋之下可以說有點過度設計。 這件事暫時沒有立即的影響， 而我也沒空處理， 因此就擱著， 打算等到哪天我有空再來重構。 不過基於如此前車之鑑，新網頁盡可能地簡約。

雖然有了新網頁， 不過還是會在這裡繼續寫週記， 至於英文筆記（會有嗎）就會改到新網頁上。

代理變數

這是一篇用來幫助我思考代理變數的中文筆記， 所有內容幾乎都是參考 Tchetgen Tchetgen et al. (2024)。

假設我們觀察到一筆 IID 的資料 \(\{(A_i, L_i, Y_i)\}_{i=1}^n\) 從 \((A, L, Y)\) 的分配中抽出， 其中 \(A\) 是一個二元處理（treatment）變數， \(L\) 是共變數（covariate）， \(Y\) 是一個結果變數。 令 \(Y_a\) 是處理狀態為 \(a\) 時的潛在結果（potential outcome）。 假設一致性（causal consistency）成立 \(Y = Y_A\)。 我們的目標是估計 \(A\) 對 \(Y\) 的平均因果效應， 如 \[ \operatorname{E}(Y_1 - Y_0). \qquad{(1)}\] 標準的假設是沒有觀察不到的干擾因子（no unmeasured confounding）， 即 \[ Y_a \perp\!\!\!\perp A \mid L, \quad a \in \{0, 1\}, \] 而且正值性（positicity）假設， 即對所有 \(a\) 和 \(l\)， \[ p(a \mid l) > 0 \qquad{(2)}\] 成立 （用 \(p\) 表示機率密度函數或機率質量函數）。 給定 Equation 1 與 Equation 2， 我們有 \[ \begin{aligned} \operatorname{E}(Y_a) &= \sum_l \operatorname{E}(Y_a \mid l) p(l) \\ &= \sum_l \operatorname{E}(Y_a \mid a, l) p(l) \\ &= \sum_l \operatorname{E}(Y \mid a, l) p(l). \end{aligned} \qquad{(3)}\] 這個式子被 James Robins 稱為 g-formula， 而也被稱為後門調整公式（backdoor adjustment formula）。

現在我們來考慮一個資料生成機制，由下圖描述。

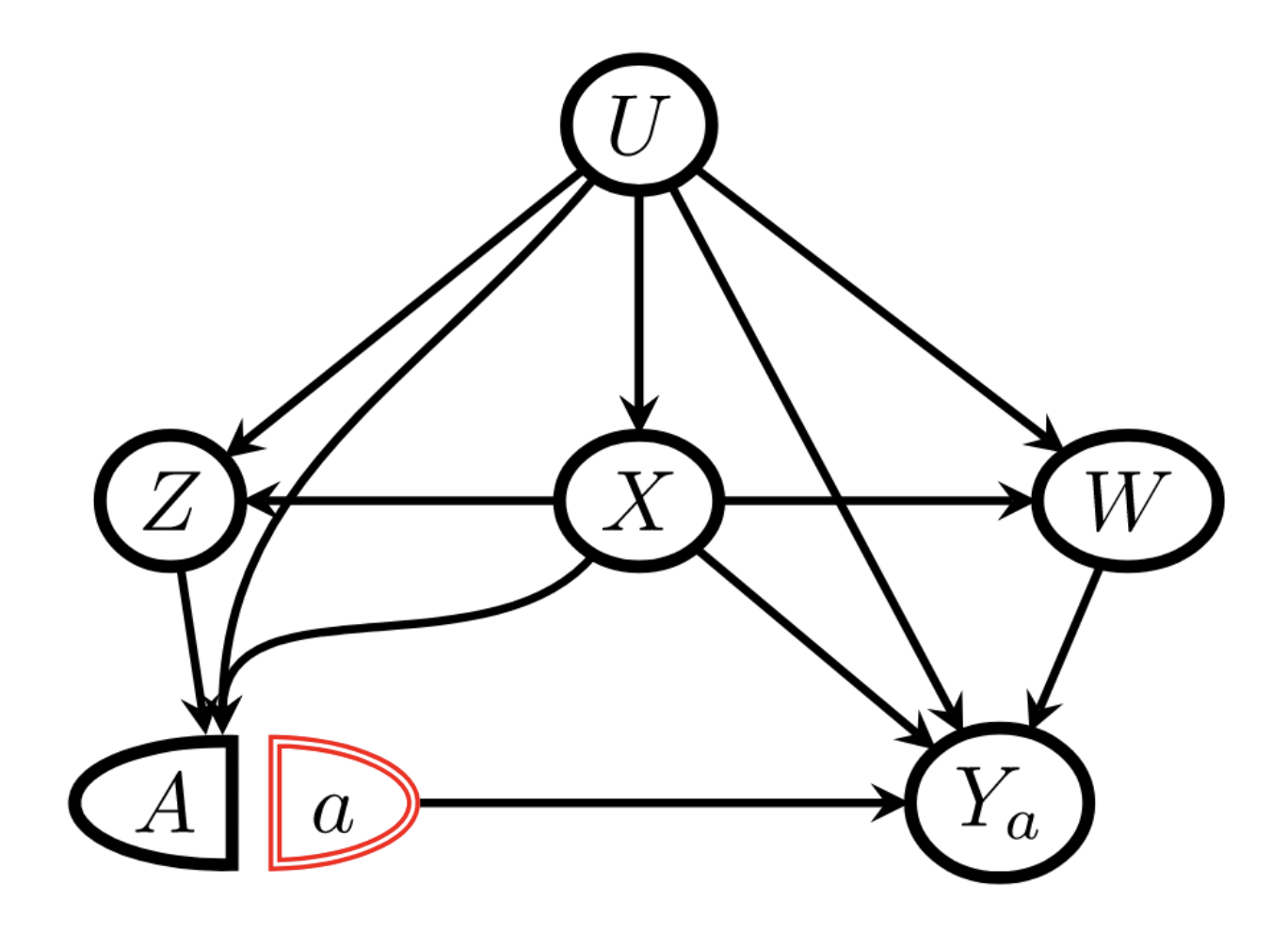
Figure 1: 有無法觀察到的干擾因子。圖出自 Tchetgen Tchetgen et al. (2024)。

在 Figure 1 這個 single world intervention graph (SWIG) 中， \(U\) 是一個無法觀察到的干擾因子， 而共變數 \(L = (X, Z, W)\)。 這個 SWIG 並蘊含了 \[ (W, Y_a) \perp\!\!\!\perp (A, Z) \mid (U, X), \quad a \in \{0, 1\}, \qquad{(4)}\] 根據 weak union 的性質，1 這隱含 \[ (W, Y_a) \perp\!\!\!\perp Z \mid (A, U, X), \quad a \in \{0, 1\}. \]

令 \(h(a, x, w)\) 是以下方程式的解： \[ \operatorname{E}(Y \mid a, z, x) = \sum_w h(a, x, w) p(w \mid a, x, z). \qquad{(5)}\] 其中 \(\sum_w\) 是對 \(W\) 的求和或積分， 而 \(h\) 稱為 outcome confounding bridge function。 假設以下完備性（completeness）條件成立： 對於任意 \(v \in L_2\)， \[ \operatorname{E}[v(U) \mid Z, A, X] = 0 \text{ a.s. } \implies v(U) = 0 \text{ a.s.} \qquad{(6)}\]

那麼在一致性、正值性、Equation 4、 Equation 5 與 Equation 6 成立的情況下， \[ \operatorname{E}(Y_a) = \sum_{w, x} h(a, x, w) p(w, x). \qquad{(7)}\] 這個式子被稱為 proximal g-formula。

以下我們從線性模型的例子來理解 Equation 7。

線性結構模型的情況

假設 Figure 1 背後的因果模型包括以下的線性結構方程式： \[ \begin{aligned} Y &= \beta_0 + \beta_a A + \beta_x X + \beta_u U + \beta_w W + \varepsilon_Y, \\ W &= \eta_0 + \eta_x X + \eta_u U + \varepsilon_W, \end{aligned} \] 其中 \(\varepsilon_Y\) 與 \(\varepsilon_W\) 是相互獨立的誤差項。 根據上式，我們有 \[ \begin{aligned} \operatorname{E}(Y \mid A, Z, X) &= \beta_0 + \beta_a A + \beta_x X + \beta_u \operatorname{E}(U \mid A, Z, X) + \beta_w \operatorname{E}(W \mid A, Z, X), \\ \operatorname{E}(W \mid A, Z, X) &= \eta_0 + \eta_x X + \eta_u \operatorname{E}(U \mid A, Z, X). \end{aligned} \] 移項以後可以得到 \[ \operatorname{E}(U \mid A, Z, X) = \frac{1}{\eta_u} \operatorname{E}(W \mid A, Z, X) - \frac{\eta_0}{\eta_u} - \frac{\eta_x}{\eta_u} X, \] 而將上式代入 \(\operatorname{E}(Y \mid A, Z, X)\) 可得 \[ \begin{aligned} &\mathrel{\phantom{=}} \operatorname{E}(Y \mid A, Z, X) \\ &= \underbrace{\left(\beta_0 - \frac{\beta_u \eta_0}{\eta_u}\right)}_{\beta_0^*} + \beta_a A + \underbrace{\left(\beta_x - \frac{\beta_u \eta_x}{\eta_u}\right)}_{\beta_x^*} X + \underbrace{\left(\beta_w + \frac{\beta_u}{\eta_u}\right)}_{\beta_w^*} \operatorname{E}(W \mid A, Z, X) \\ &= \beta_0^* + \beta_a A + \beta_x^* X + \beta_w^* \operatorname{E}(W \mid A, Z, X). \end{aligned} \] 此時，Equation 5 的解是 \[ h(a, x, w) = \beta_0^* + \beta_a a + \beta_x^* x + \beta_w^* w. \]

這給我們幾個啟示：

  1. 我們可以用 2SLS 來估計 \(\beta_a\)：

    1. 以 \(W\) 對 \((A, Z, X)\) 做線性迴歸， 取得 \(\hat{W} = \hat{\eta}_0 + \hat{\eta}_a A + \hat{\eta}_z Z + \hat{\eta}_x X\)。

    2. 以 \(Y\) 對 \((A, X, \hat{W})\) 做線性迴歸， 而 \(\hat{\beta}_a\) 就是 \(\beta_a\) 的一致估計（在線性結構模型成立的情況下）。

    這種方法被稱為 proximal 2SLS (P2SLS)。

  2. 既然 2SLS 和 control function 的方法是一體兩面， 那我們也可以利用 control function 來估計 \(\beta_a\)：

    1. 以 \(W\) 對 \((A, Z, X)\) 做線性迴歸， 取得殘差 \(\tilde{W} = W - \hat{W}\)。

    2. 以 \(Y\) 對 \((A, X, W, \tilde{W})\) 做線性迴歸， 而 \(A\) 的迴歸係數就是 \(\beta_a\) 的一致估計。

  3. 如果 \(U\) 不影響 \(Y\)，即 \(\beta_u = 0\)， 也就沒有觀察不到的干擾因子， 那麼 \(\beta_0 = \beta_0^*\)、\(\beta_x = \beta_x^*\) 與 \(\beta_w = \beta_w^*\)。 此時，直接以 \(Y\) 對 \((A, X, W)\) 做線性迴歸， 就可以得到 \(\beta_a\) 的一致估計。 不過，就算我們使用 P2SLS， 我們也還是可以得到 \(\beta_a\) 的一致估計。

  1. 參見 Graphoid。↩︎